四次元多胞体の一覧表について　　about Four-dimensional Polytopes

四次元多胞体の三次元投影ビューアは、多胞体の表示内容をいろいろと変更表示できるビューアです。ビューアの詳細な使用方法については、上のメニューの「Polytope Viewer」をクリックして参照下さい。作成した多胞体は、胞，面，稜，頂点の各オブジェクトから構成されます。ビューアでは、コントローパネルで回転モード，投影方法，各オブジェクトのプロパティおよび表示／非表示を切替えることにより多胞体を表示します。 　以下に示す多胞体の一覧表においては、以下の６種類の典型的な表示設定をリンクとして設定しています（表示設定は、ビューアを１回起動すれば、コントローパネルですべて設定可能ですが、慣れないと扱いにくいためこのような設定としています）。なお、以下の表示設定では、回転モードがずべて「3Dモード」で起動します。これは、「4Dモード」では、回転中に形状（頂点座標）が随時変化するため、複雑な多胞体（特に正百二十胞体，正六珀胞体）では動作が重くなり反応が追いつかない場合があるからです。これらの動作環境は、お使いのPCのグラフィックス性能によりますので、「4Dモード」に切替える場合は、最初は比較的単純な多胞体（正五胞体～正二十四多胞体）で確認しながら行うことをおすすめします（動作が重たい場合でも時間がかかるだけで最終的には表示されると思いますが）。 　　(1) 面・円柱表示中心投影＝3Dモード・中心投影・面表示・稜：円柱表示・頂点：球表示 　　(2) 面・円柱表示平行投影＝3Dモード・平行投影・面表示・稜：円柱表示・頂点：球表示 　　(3) 胞・円柱表示中心投影＝3Dモード・中心投影・胞表示・稜：円柱表示・頂点：球表示 　　(4) 胞・Line表示中心投影＝3Dモード・中心投影・胞表示・稜：Line表示・頂点：球表示 　　(5) 骨格円柱表示中心投影＝3Dモード・中心投影・胞面非表示・稜：円柱表示・頂点：球表示 　　(6) 骨格Line表示中心投影＝3Dモード・中心投影・胞面非表示・稜：Line表示・頂点：球表示 　ビューアを起動すると、中央に多胞体が表示されますが、これをマウスでドラッグ（左クリックしたまま移動する）すると、図形が回転します。図形の拡大／縮小はマウスのホイールボタンでできます。

正多胞体　　Regular polytopes 胞数：N3, 面数：N2, 稜数：N1, 頂点数：N0, 稜長：a, 外接球半径：R1, 内接球半径：R0
正五胞体（四次元正単体）　　Regular 5-cell　　{3,3,3}　　自己双対 構成胞：正四面体，構成面：正三角形，対応する三次元多面体：正四面体 N3=5, N2=10, N1=10, N0=5, R1/a=√(2/5), R0/a=√10/20, R1/R0=4
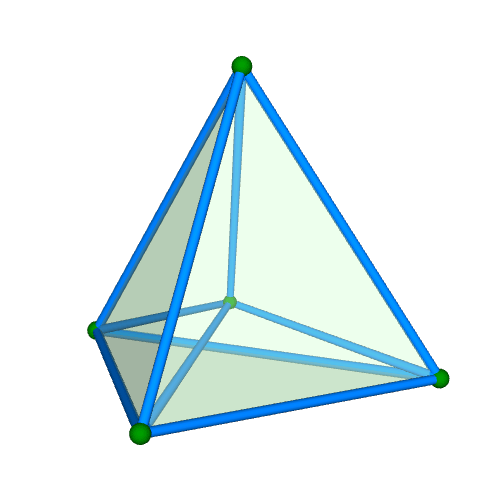面・円柱表示 中心投影	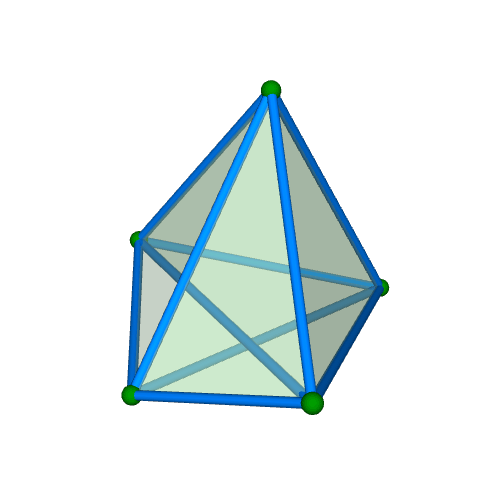面・円柱表示 平行投影	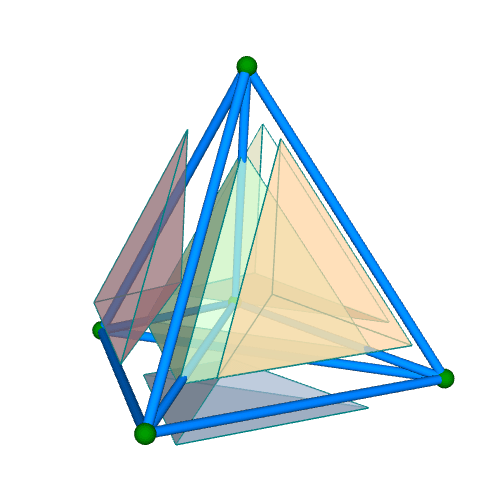胞・円柱表示 中心投影	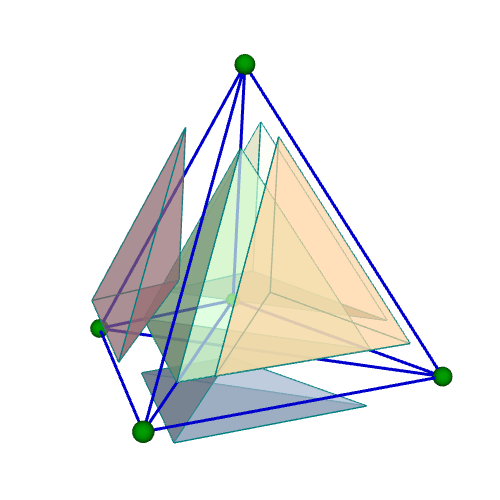胞・Line表示 中心投影	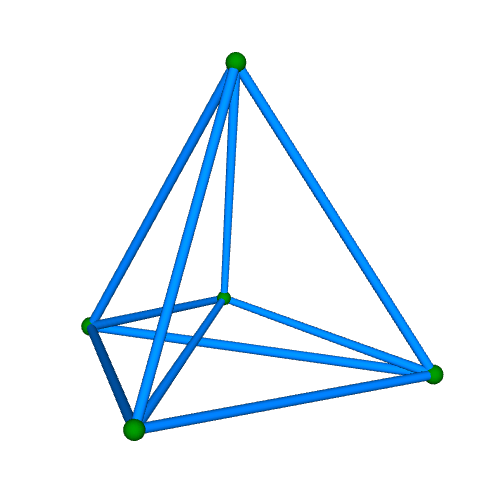骨格円柱表示 中心投影	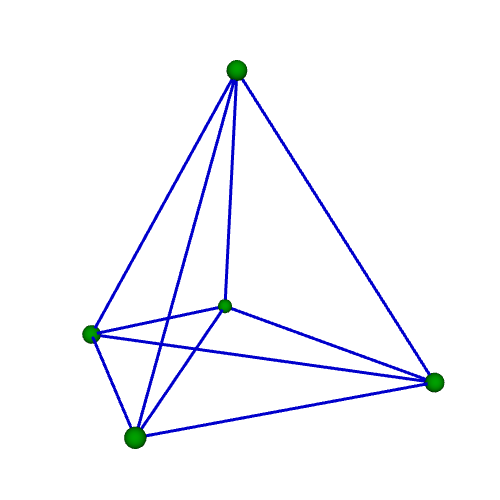骨格Line表示 中心投影
正八胞体（四次元正則体，四次元超立方体）　　Regular 8-cell　　{4,3,3}　　双対：正十六胞体 構成胞：正六面体，構成面：正方形，対応する三次元多面体：正六面体 N3=8, N2=24, N1=32, N0=16, R1/a=1, R0/a=1/2, R1/R0=2
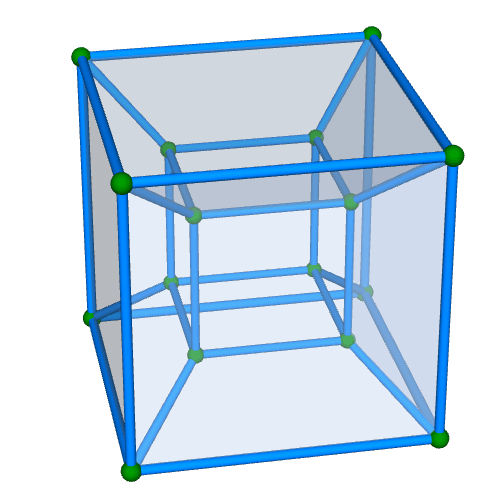面・円柱表示 中心投影	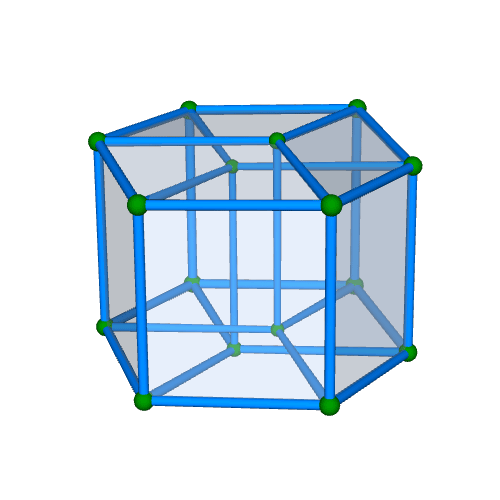面・円柱表示 平行投影	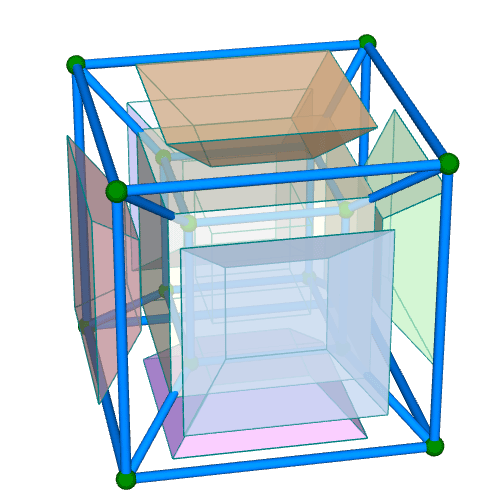胞・円柱表示 中心投影	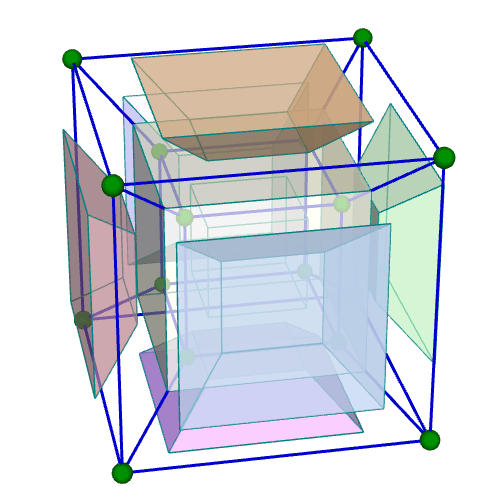胞・Line表示 中心投影	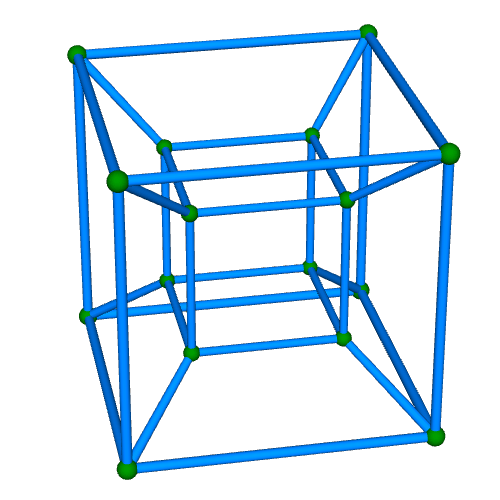骨格円柱表示 中心投影	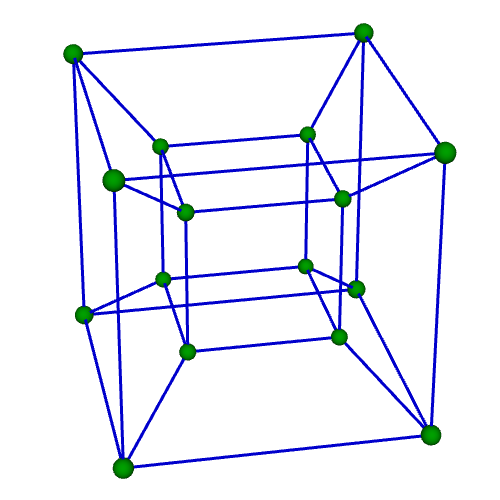骨格Line表示 中心投影
正十六胞体（四次元正軸体）　　Regular 16-cell　　{3,3,4}　　双対：正八胞体 構成胞：正四面体，構成面：正三角形，対応する三次元多面体：正八面体 N3=16, N2=32, N1=24, N0=8, R1/a=1/√2, R0/a=1/2√2, R1/R0=2
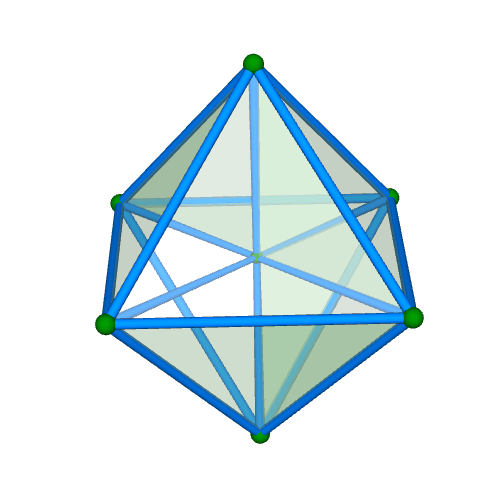面・円柱表示 中心投影	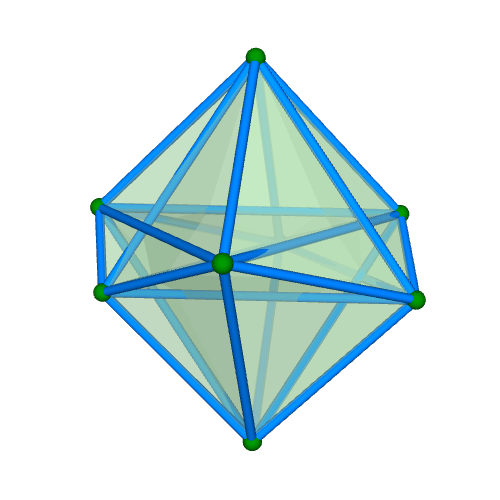面・円柱表示 平行投影	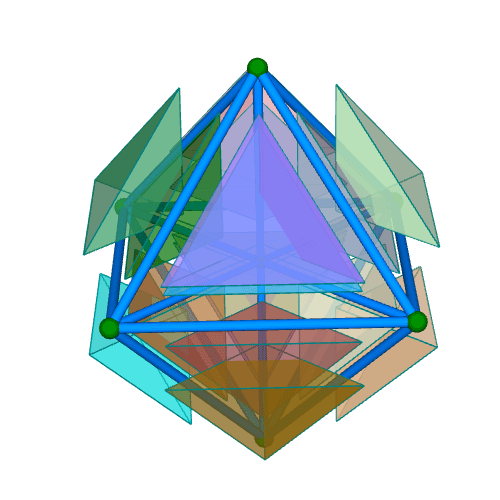胞・円柱表示 中心投影	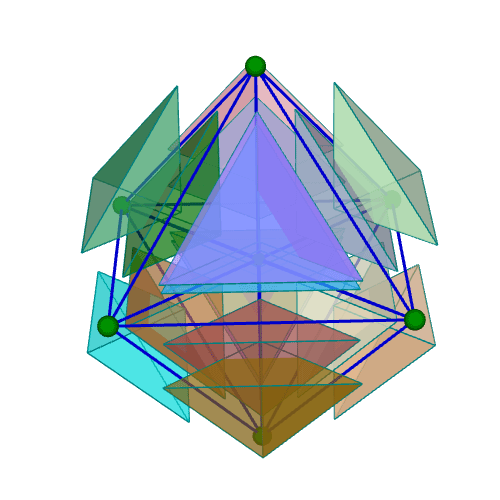胞・Line表示 中心投影	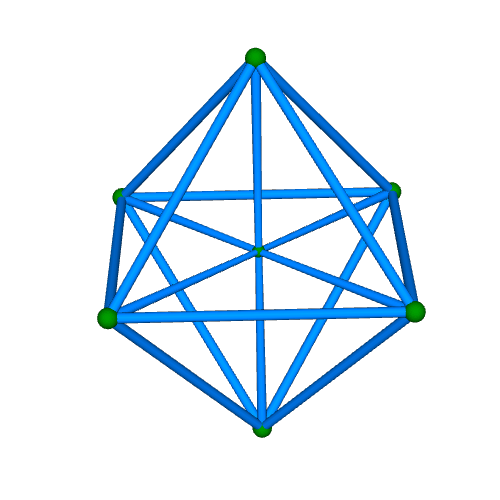骨格円柱表示 中心投影	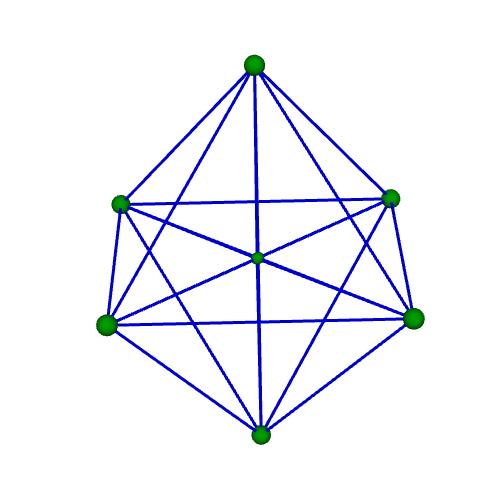骨格Line表示 中心投影
正二十四胞体　　Regular 24-cell　　{3,4,3}　　自己双対 構成胞：正八面体，構成面：正三角形，対応する三次元多面体：菱形十二面体 N3=24, N2=96, N1=96, N0=24, R1/a=1, R0/a=1/√2, R1/R0=√2
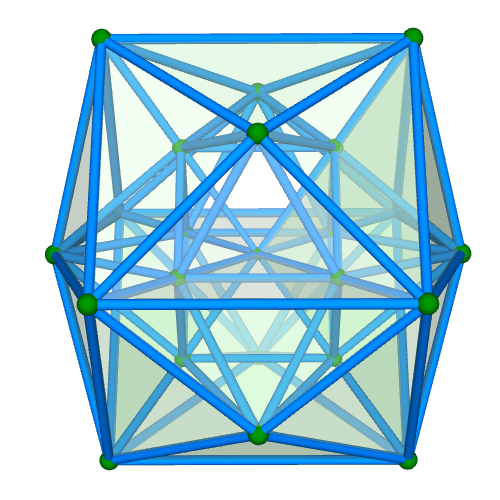面・円柱表示 中心投影	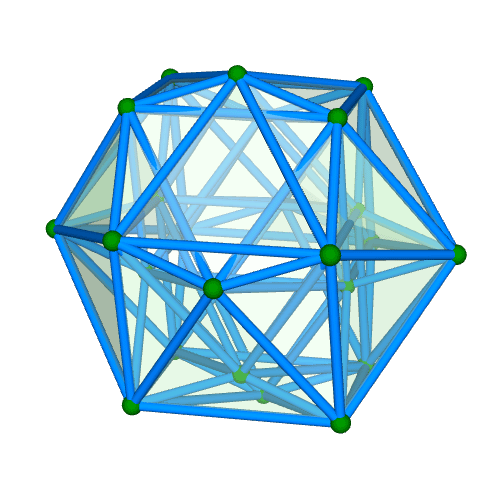面・円柱表示 平行投影	胞・円柱表示 中心投影	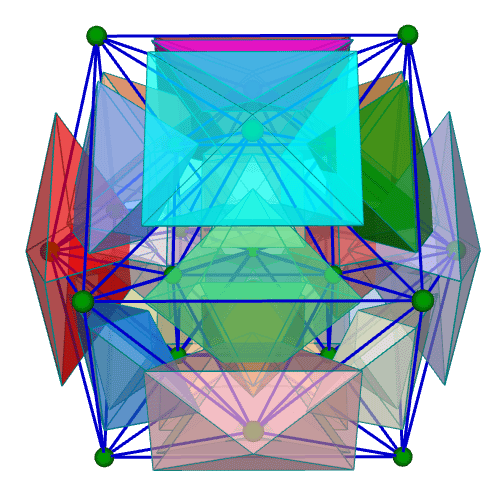胞・Line表示 中心投影	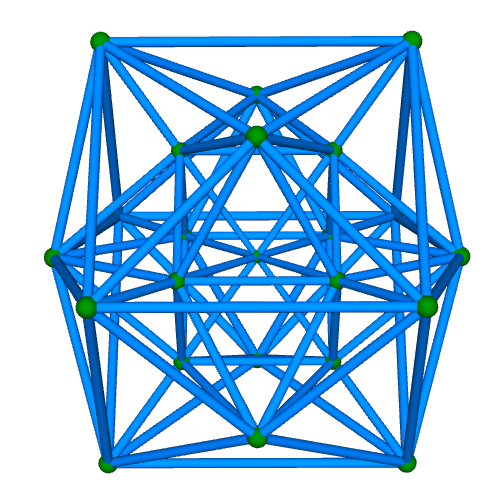骨格円柱表示 中心投影	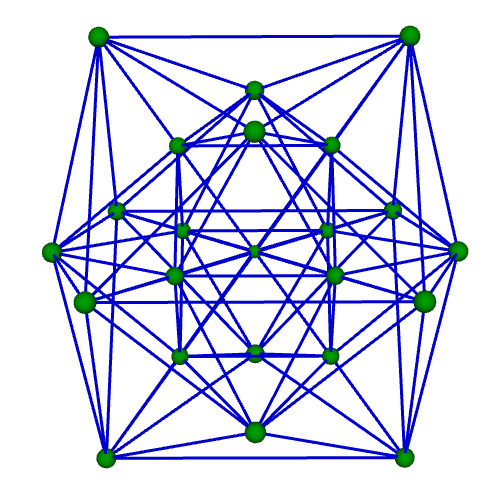骨格Line表示 中心投影
正百二十胞体　　Regular 120-cell　　{5,3,3}　　双対：正六百胞体 構成胞：正十二面体，構成面：正五角形，対応する三次元多面体：正十二面体 N3=120, N2=720, N1=1200, N0=600, R1/a=√2(3+√5)/2, R0/a=(7+3√5)/4, R1/R0=√2(3-√5)
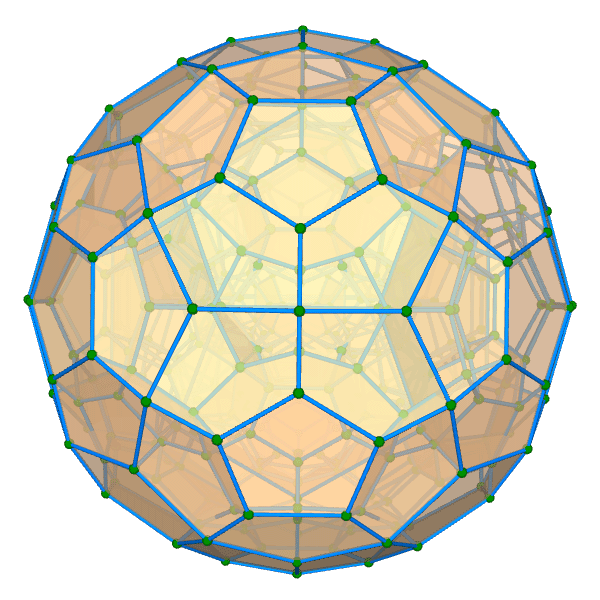面・円柱表示 中心投影	面・円柱表示 平行投影	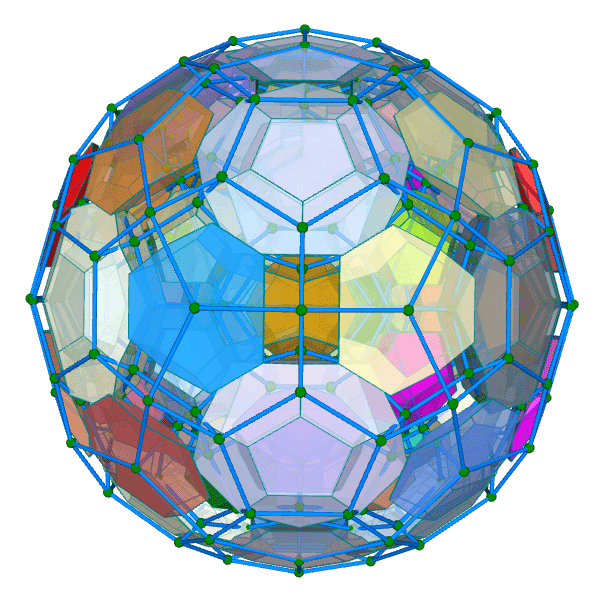胞・円柱表示 中心投影	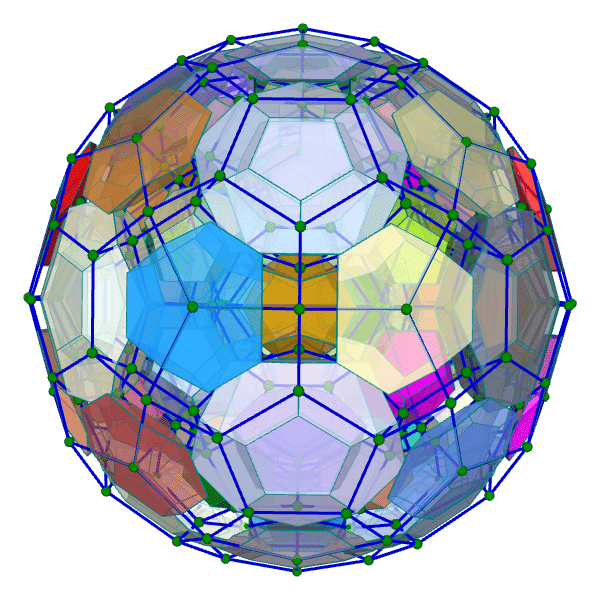胞・Line表示 中心投影	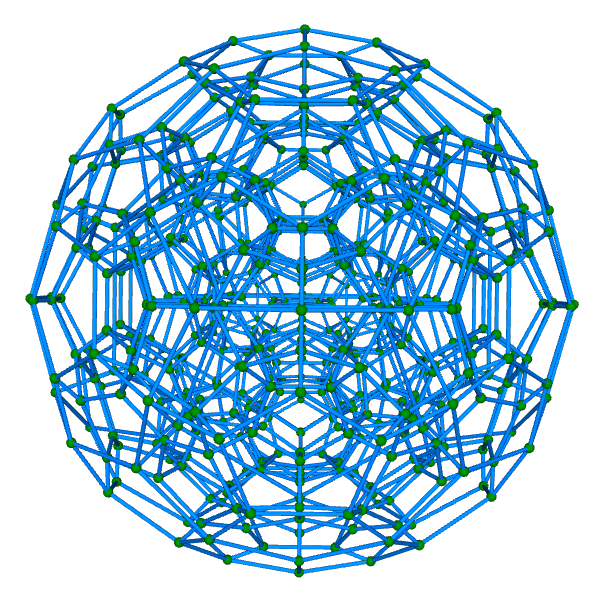骨格円柱表示 中心投影	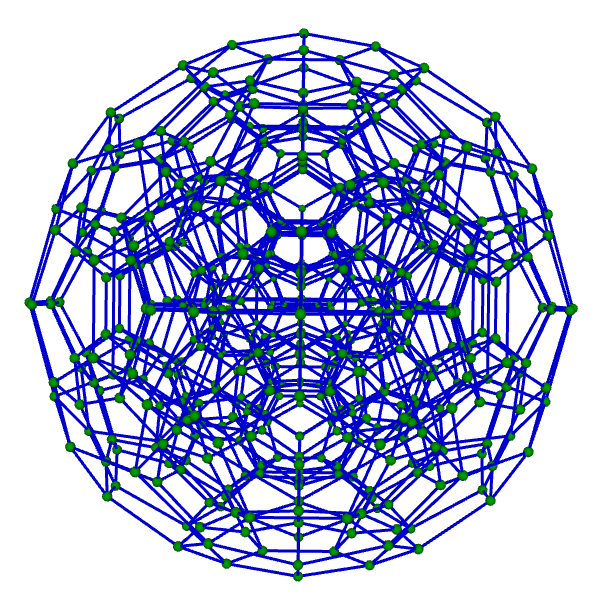骨格Line表示 中心投影
正六百胞体　　Regular 600-cell　　{3,3,5}　　双対：正百二十胞体 構成胞：正四面体，構成面：正三角形，対応する三次元多面体：正二十面体 N3=600, N2=1200, N1=720, N0=120, R1/a=(1+√5)/2, R0/a=(2+√5)/2√2, R1/R0=√2(3-√5)
面・円柱表示 中心投影	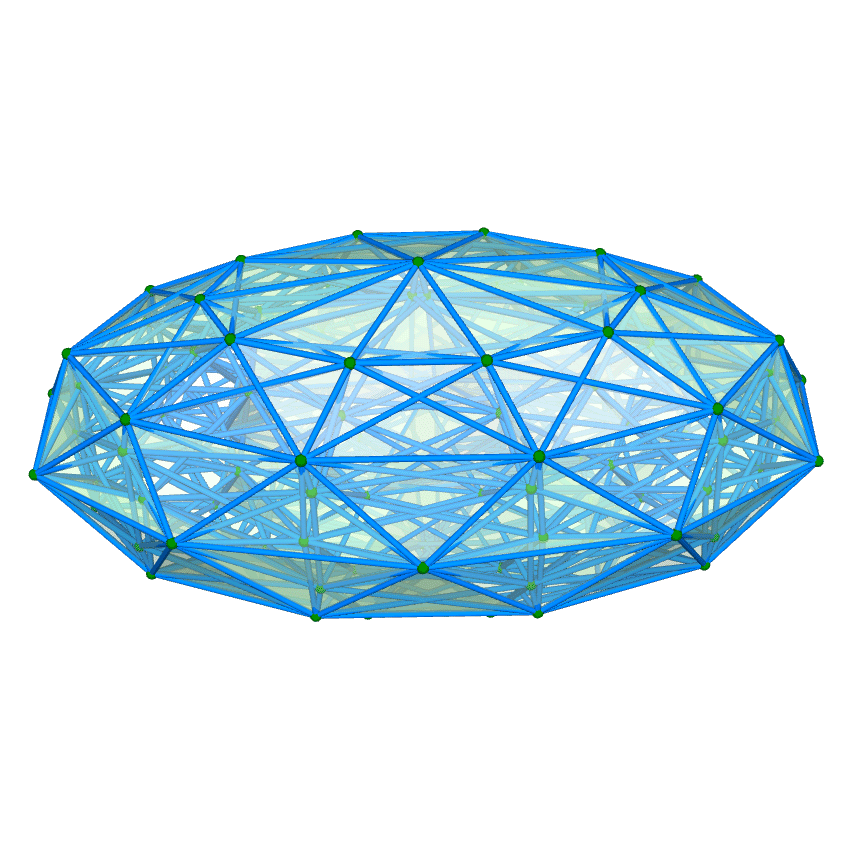面・円柱表示 平行投影	胞・円柱表示 中心投影	胞・Line表示 中心投影	骨格円柱表示 中心投影	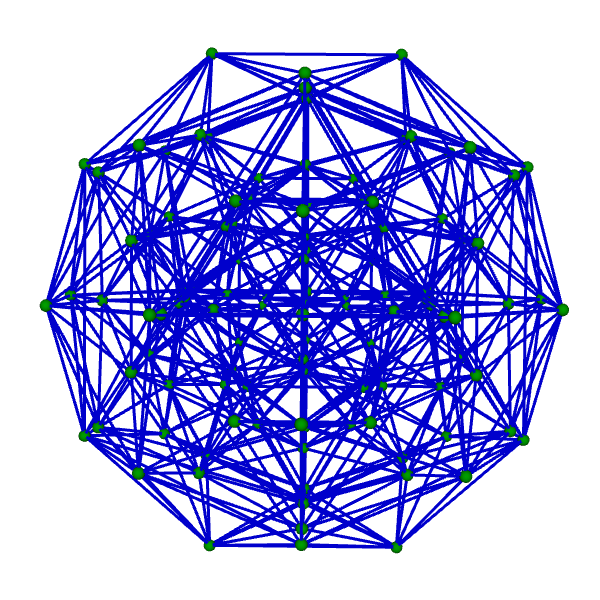骨格Line表示 中心投影

ページトップへ　　Jump to Top